Table Of Contents

Commands frame:/loopy_belief_propagation

Message passing to infer state probabilities.

POST /v1/commands/

GET /v1/commands/:id

Request

Route

POST /v1/commands/

Body

name:

frame:/loopy_belief_propagation
arguments:

frame : <bound method AtkEntityType.__name__ of <trustedanalytics.rest.jsonschema.AtkEntityType object at 0x7f9e686f3fd0>>

<Missing Description>

src_col_name : unicode

The column name for the source vertex id.

dest_col_name : unicode

The column name for the destination vertex id.

weight_col_name : unicode

The column name for the edge weight.

src_label_col_name : unicode

The column name for the label properties for the source vertex.

result_col_name : unicode (default=None)

The column name for the results (holding the post labels for the vertices).

ignore_vertex_type : bool (default=None)

If True, all vertex will be treated as training data. Default is False.

max_iterations : int32 (default=None)

The maximum number of supersteps that the algorithm will execute. The valid value range is all positive int. The default value is 10.

convergence_threshold : float32 (default=None)

The amount of change in cost function that will be tolerated at convergence. If the change is less than this threshold, the algorithm exits earlier before it reaches the maximum number of supersteps. The valid value range is all float and zero. The default value is 0.00000001f.

anchor_threshold : float64 (default=None)

The parameter that determines if a node’s posterior will be updated or not. If a node’s maximum prior value is greater than this threshold, the node will be treated as anchor node, whose posterior will inherit from prior without update. This is for the case where we have confident prior estimation for some nodes and don’t want the algorithm to update these nodes. The valid value range is in [0, 1]. Default is 1.0.

smoothing : float32 (default=None)

The Ising smoothing parameter. This parameter adjusts the relative strength of closeness encoded edge weights, similar to the width of Gaussian distribution. Larger value implies smoother decay and the edge weight becomes less important. Default is 2.0.

max_product : bool (default=None)

Should LBP use max_product or not. Default is False.

power : float32 (default=None)

Power coefficient for power edge potential. Default is 0.

Headers

Authorization: test_api_key_1
Content-type: application/json

Description

Loopy belief propagation on Markov Random Fields (MRF). Belief Propagation (BP) was originally designed for acyclic graphical models, then it was found that the BP algorithm can be used in general graphs. The algorithm is then sometimes called “Loopy” Belief Propagation (LBP), because graphs typically contain cycles, or loops.

Loopy Belief Propagation (LBP)

Loopy Belief Propagation (LBP) is a message passing algorithm for inferring state probabilities, given a graph and a set of noisy initial estimates. The LBP implementation assumes that the joint distribution of the data is given by a Boltzmann distribution.

For more information about LBP, see: “K. Murphy, Y. Weiss, and M. Jordan, Loopy-belief Propagation for Approximate Inference: An Empirical Study, UAI 1999.”

LBP has a wide range of applications in structured prediction, such as low-level vision and influence spread in social networks, where we have prior noisy predictions for a large set of random variables and a graph encoding relationships between those variables.

The algorithm performs approximate inference on an undirected graph of hidden variables, where each variable is represented as a node, and each edge encodes relations to its neighbors. Initially, a prior noisy estimate of state probabilities is given to each node, then the algorithm infers the posterior distribution of each node by propagating and collecting messages to and from its neighbors and updating the beliefs.

In graphs containing loops, convergence is not guaranteed, though LBP has demonstrated empirical success in many areas and in practice often converges close to the true joint probability distribution.

Discrete Loopy Belief Propagation

LBP is typically considered a semi-supervised machine learning algorithm as

  1. there is typically no ground truth observation of states
  2. the algorithm is primarily concerned with estimating a joint probability function rather than with classification or point prediction.

The standard (discrete) LBP algorithm requires a set of probability thresholds to be considered a classifier. Nonetheless, the discrete LBP algorithm allows Test/Train/Validate splits of the data and the algorithm will treat “Train” observations differently from “Test” and “Validate” observations. Vertices labeled with “Test” or “Validate” will be treated as though they have uninformative (uniform) priors and are allowed to receive messages, but not send messages. This simulates a “scoring scenario” in which a new observation is added to a graph containing fully trained LBP posteriors, the new vertex is scored based on received messages, but the full LBP algorithm is not repeated in full. This behavior can be turned off by setting the ignore_vertex_type parameter to True. When ignore_vertex_type=True, all nodes will be considered “Train” regardless of their sample type designation. The Gaussian (continuous) version of LBP does not allow Train/Test/Validate splits.

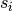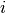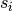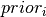The standard LBP algorithm included with the toolkit assumes an ordinal and cardinal set of discrete states. For notational convenience, we’ll denote the value of state s_{i} as i, and the prior probability of state s_{i} as prior_{i}.

Each node sends out initial messages of the form:

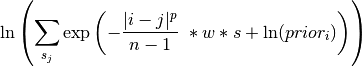
\ln \left ( \sum_{s_{j}} \exp \left ( - \frac { | i - j | ^{p} }{ n - 1 } \ * w * s + \ln (prior_{i}) \right ) \right )

Where

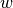  • w is the weight between the messages destination and origin vertices
  • s is the smoothing parameter
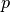  • p is the power parameter
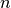  • n is the number of states

The larger the weight between two nodes, or the higher the smoothing parameter, the more neighboring vertices are assumed to “agree” on states. We represent messages as sums of log probabilities rather than products of non-logged probabilities which makes it easier to subtract messages in the future steps of the algorithm. Also note that the states are cardinal in the sense that the “pull” of state 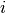i on state 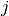j depends on the distance between 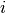i and j. 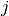The power parameter intensifies the rate at which the pull of distant states drops off.

In order for the algorithm to work properly, all edges of the graph must be bidirectional. In other words, messages need to be able to flow in both directions across every edge. Bidirectional edges can be enforced during graph building, but the LBP function provides an option to do an initial check for bidirectionality using the bidirectional_check=True option. If not all the edges of the graph are bidirectional, the algorithm will return an error.

Look at a case where a node has two states, 0 and 1. The 0 state has a prior probability of 0.9 and the 1 state has a prior probability of 0.2. The states have uniform weights of 1, power of 1 and a smoothing parameter of 2. The nodes initial message would be \textstyle \left [ \ln \left ( 0.2 \ + 0.8 e ^{-2} \right ), \ln \left ( 0.8 + 0.2 e ^{-2} \right ) \right ], which gets sent to each of that node’s neighbors. Note that messages will typically not be proper probability distributions, hence each message is normalized so that the probability of all states sum to 1 before being sent out. For simplicity of discussion, we will consider all messages as normalized messages.

After nodes have sent out their initial messages, they then update their beliefs based on messages that they have received from their neighbors, denoted by the set 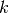k.

Updated Posterior Beliefs:

\ln (newbelief) = \propto \exp \left [ \ln (prior) + \sum_k message _{k} \ \right ]

Note that the messages in the above equation are still in log form. Nodes then send out new messages which take the same form as their initial messages, with updated beliefs in place of priors and subtracting out the information previously received from the new message’s recipient. The recipient’s prior message is subtracted out to prevent feedback loops of nodes “learning” from themselves.

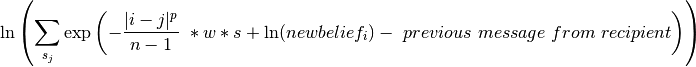
\ln \left ( \sum_{s_{j}} \exp \left ( - \frac { | i - j | ^{p} }{ n - 1 } \ * w * s + \ln (newbelief_{i}) - \ previous\ message\ from\ recipient \right ) \right )

In updating beliefs, new beliefs tend to be most influenced by the largest message. Setting the max_product option to “True” ignores all incoming messages other than the strongest signal. Doing this results in approximate solutions, but requires significantly less memory and run-time than the more exact computation. Users should consider this option when processing power is a constraint and approximate solutions to LBP will be sufficient.

This process of updating and message passing continues until the convergence criteria is met or the maximum number of supersteps is reached without converging. A node is said to converge if the total change in its distribution (the sum of absolute value changes in state probabilities) is less than the convergence_threshold parameter. Convergence is a local phenomenon; not all nodes will converge at the same time. It is also possible for some (most) nodes to converge and others to never converge. The algorithm requires all nodes to converge before declaring that the algorithm has converged overall. If this condition is not met, the algorithm will continue up to the maximum number of supersteps.

See: http://en.wikipedia.org/wiki/Belief_propagation.


Response

Status

200 OK

Body

Returns information about the command. See the Response Body for Get Command here below. It is the same.

GET /v1/commands/:id

Request

Route

GET /v1/commands/18

Body

(None)

Headers

Authorization: test_api_key_1
Content-type: application/json

Response

Status

200 OK

Body

dict

a 2-column frame:

vertex: int
A vertex id.
result : Vector (long)
label vector for the results (for the node id in column 1).
  • © Copyright 2015, Intel.
  • Last updated on Sep 24, 2015.