Frame label_propagation

---

label_propagation(self, src_col_name, dest_col_name, weight_col_name, src_label_col_name, result_col_name=None, max_iterations=None, convergence_threshold=None, alpha=None)

Label Propagation on Gaussian Random Fields.

Parameters:

src_col_name : unicode

The column name for the source vertex id.

dest_col_name : unicode

The column name for the destination vertex id.

weight_col_name : unicode

The column name for the edge weight.

src_label_col_name : unicode

The column name for the label properties for the source vertex.

result_col_name : unicode (default=None)

The column name for the results (holding the post labels for the vertices).

max_iterations : int32 (default=None)

The maximum number of supersteps that the algorithm will execute. The valid value range is all positive int. Default is 10.

convergence_threshold : float32 (default=None)

The amount of change in cost function that will be tolerated at convergence. If the change is less than this threshold, the algorithm exits earlier before it reaches the maximum number of supersteps. The valid value range is all float and zero. Default is 0.00000001f.

alpha : float32 (default=None)

The tradeoff parameter that controls how much influence an external classifier’s prediction contributes to the final prediction. This is for the case where an external classifier is available that can produce initial probabilistic classification on unlabeled examples, and the option allows incorporating external classifier’s prediction into the LP training process. The valid value range is [0.0,1.0]. Default is 0.

Returns:

: dict

A 2-column frame:

vertex: int

A vertex id.

result : Vector (long)

label vector for the results (for the node id in column 1)

Label Propagation on Gaussian Random Fields.

This algorithm is presented in X. Zhu and Z. Ghahramani. Learning from labeled and unlabeled data with label propagation. Technical Report CMU-CALD-02-107, CMU, 2002.

Label Propagation (LP)

LP is a message passing technique for inputing or smoothing labels in partially-labeled datasets. Labels are propagated from labeled data to unlabeled data along a graph encoding similarity relationships among data points. The labels of known data can be probabilistic, in other words, a known point can be represented with fuzzy labels such as 90% label 0 and 10% label 1. The inverse distance between data points is represented by edge weights, with closer points having a higher weight (stronger influence on posterior estimates) than points farther away. LP has been used for many problems, particularly those involving a similarity measure between data points. Our implementation is based on Zhu and Ghahramani’s 2002 paper, Learning from labeled and unlabeled data..

The Label Propagation Algorithm

In LP, all nodes start with a prior distribution of states and the initial messages vertices pass to their neighbors are simply their prior beliefs. If certain observations have states that are known deterministically, they can be given a prior probability of 100% for their true state and 0% for all others. Unknown observations should be given uninformative priors.

Each node, 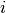, receives messages from its 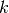neighbors and updates its beliefs by taking a weighted average of its current beliefs and a weighted average of the messages received from its neighbors.

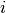The updated beliefs for node are: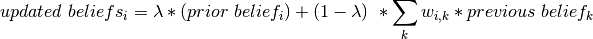

where 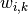is the normalized weight between nodes 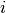and 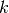, normalized such that the sum of all weights to neighbors is 1.

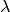is a leaning parameter. If 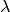is greater than zero, updated probabilities will be anchored in the direction of prior beliefs.

The final distribution of state probabilities will also tend to be biased in the direction of the distribution of initial beliefs. For the first iteration of updates, nodes’ previous beliefs are equal to the priors, and, in each future iteration, previous beliefs are equal to their beliefs as of the last iteration. All beliefs for every node will be updated in this fashion, including known observations, unless anchor_threshold is set. The anchor_threshold parameter specifies a probability threshold above which beliefs should no longer be updated. Hence, with an anchor_threshold of 0.99, observations with states known with 100% certainty will not be updated by this algorithm.

This process of updating and message passing continues until the convergence criteria is met, or the maximum number of supersteps is reached. A node is said to converge if the total change in its cost function is below the convergence threshold. The cost function for a node is given by:

Convergence is a local phenomenon; not all nodes will converge at the same time. It is also possible that some (most) nodes will converge and others will not converge. The algorithm requires all nodes to converge before declaring global convergence. If this condition is not met, the algorithm will continue up to the maximum number of supersteps.

Examples

input frame (lp.csv) “a” “b” “c” “d” 1, 2, 0.5, “0.5,0.5” 2, 3, 0.4, “-1,-1” 3, 1, 0.1, “0.8,0.2”

script

ta.connect() s = [(“a”, ta.int32), (“b”, ta.int32), (“c”, ta.float32), (“d”, ta.vector(2))] d = “lp.csv” c = ta.CsvFile(d,s) f = ta.Frame(c) r = f.label_propagation(“a”, “b”, “c”, “d”, “results”) r[‘frame’].inspect() r[‘report’]

The expected output is like this:

{u'value': u'======Graph Statistics======\nNumber of vertices: 600\nNumber of edges: 15716\n\n======LP Configuration======\nlambda: 0.000000\nanchorThreshold: 0.900000\nconvergenceThreshold: 0.000000\nmaxSupersteps: 10\nbidirectionalCheck: false\n\n======Learning Progress======\nsuperstep = 1\tcost = 0.008692\nsuperstep = 2\tcost = 0.008155\nsuperstep = 3\tcost = 0.007809\nsuperstep = 4\tcost = 0.007544\nsuperstep = 5\tcost = 0.007328\nsuperstep = 6\tcost = 0.007142\nsuperstep = 7\tcost = 0.006979\nsuperstep = 8\tcost = 0.006833\nsuperstep = 9\tcost = 0.006701\nsuperstep = 10\tcost = 0.006580'}